Counting Prime Numbers: Classic vs. Sieve of Eratosthenes

Counting prime numbers is a fundamental problem in programming. While a classical approach is the first choice for many, the efficiency of the algorithm matters. In this blog post, we’ll explore two approaches for solving this problem and compare their performance.

Understanding Prime Numbers

Prime numbers are integers divisible only by 1 and themselves. We’ll count these unique numbers within a given range.

Classic Approach

The classic approach involves checking each number within the range to determine if it’s prime. We use a simple isPrime function for this purpose. Here’s the code:

def isPrime(n:int) -> bool:
  if n <= 1:
      return False
  for i in range(2,int(sqrt(n))+1):
    if n%i == 0:
      return False
  return True

def countPrimesClassic(n:int)->int:
  c = 0
  for i in range(2,n):
    if isPrime(i):
      c+=1
  return c

This classic approach works, but it can be slow for large ranges.

Sieve of Eratosthenes

The Sieve of Eratosthenes is a more efficient method for counting prime numbers. It works by systematically eliminating non-prime numbers. The algorithm is as follows:

1. Create a list of consecutive integers from \(2\) through \(n\).
2. Start with the smallest prime number, \(p = 2\).
3. Eliminate multiples of \(p\) by marking them in the list.
4. Find the smallest unmarked number greater than \(p\) and set \(p\) to this number. Repeat from step 3.
5. When the algorithm terminates, the unmarked numbers are prime below \(n\).

Here’s the code for the Sieve of Eratosthenes:

from math import sqrt
def countPrimesSieve(n: int) -> int:
    if n <= 2: return 0
    np, ans = [False]*n, 1
    for i in range(3, int(sqrt(n))+1, 2):
        if np[i]: continue
        for j in range(i*i, n, 2*i): np[j] = True
    for i in range(3, n, 2):
        if not np[i]: ans += 1
    return ans

Performance Comparison

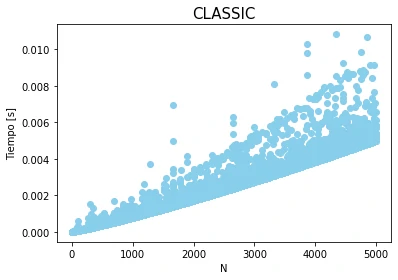
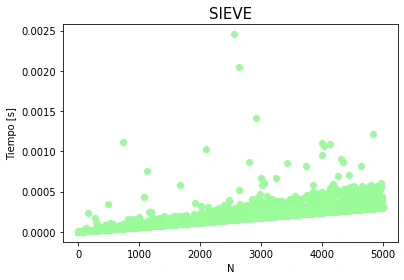
To compare the performance of these algorithms, we ran tests from 1 to 5000 with 5 samples at each iteration. The results are clear: the Sieve of Eratosthenes is faster.

Classic algorithm time

Sieve of Eratosthenes time

The Sieve of Eratosthenes takes, on average, 1 second less than the classic approach and up to 9 seconds less in the worst case.

Conclusion

Counting prime numbers is a valuable exercise in algorithm design. While this problem may not be a professional requirement, it helps reinforce mathematical concepts and encourages efficient algorithm design. By choosing the right approach, you can optimize your code and save valuable time.

If you found this post useful, don’t forget to leave your comments and questions. Follow me on social media for more content like this.