Counting Integer Partitions: Exploring a Recursive Approach
As an aspiring engineer, I regularly tackle daily code challenges to enhance my skills. I enjoyed a winning streak until I encountered the following intriguing problem.
Positive Integer Partition: Counting Partitions
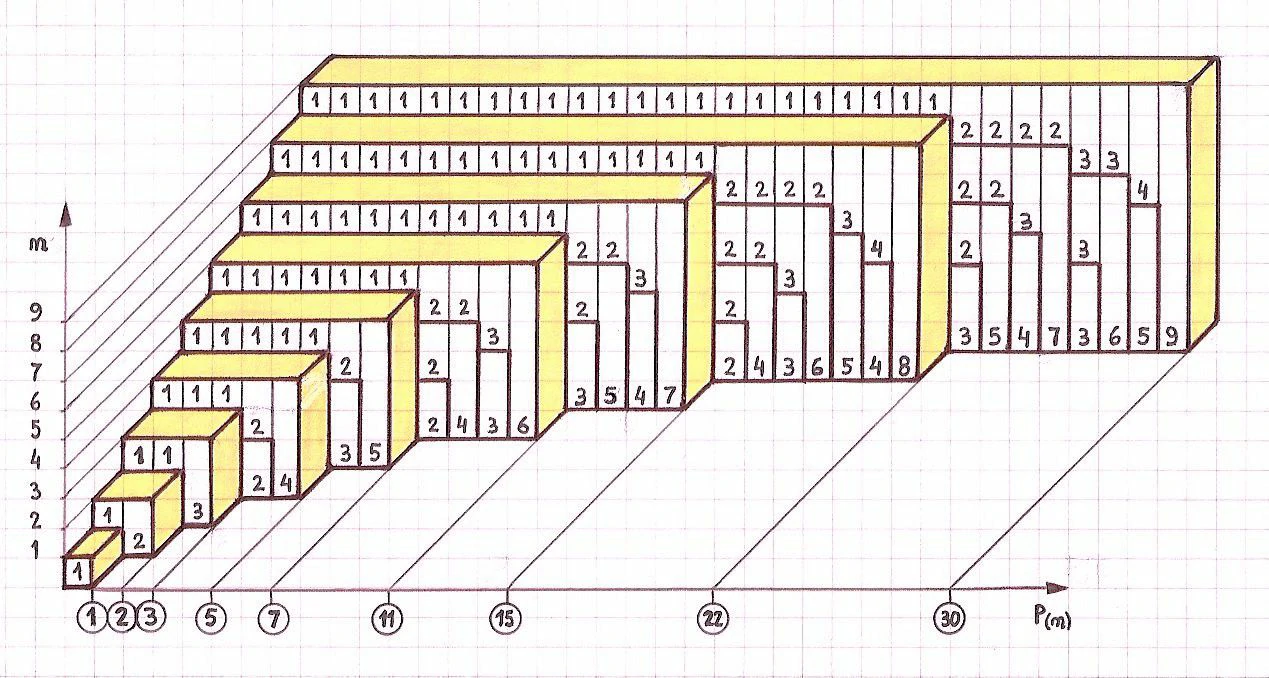
In number theory, a positive integer partition represents the sum of integer numbers. Two sums that only differ in their order are considered the same partition. Your task is to create a function that receives an integer x, and this function should return the number of distinct partitions of x.
Example
For instance, when x is 4, there are 5 different partitions:
1
2
3
4
5
[4] -> 4
[3, 1] -> 3 + 1 = 4
[2, 2] -> 2 + 2 = 4
[2, 1, 1] -> 2 + 1 + 1 = 4
[1, 1, 1, 1] -> 1 + 1 + 1 + 1 = 4
For x = 8, there are 22 distinct partitions, such as:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
[8] -> 8
[7, 1] -> 7 + 1 = 8
[6, 2] -> 6 + 2 = 8
[6, 1, 1] -> 6 + 1 + 1 = 8
[5, 3] -> 5 + 3 = 8
[5, 2, 1] -> 5 + 2 + 1 = 8
[5, 1, 1, 1] -> 5 + 1 + 1 = 8
[4, 4] -> 4 + 4 = 8
[4, 3, 1] -> 4 + 3 + 1 = 8
[4, 2, 2] -> 4 + 2 + 2 = 8
[4, 2, 1, 1] -> 4 + 2 + 1 + 1 = 8
[4, 1, 1, 1, 1] -> 4 + 1 + 1 + 1 + 1 = 8
[3, 3, 2] -> 3 + 3 + 2 = 8
[3, 3, 1, 1] -> 3 + 3 + 1 + 1 = 8
[3, 2, 2, 1] -> 3 + 2 + 2 +1 = 8
[3, 2, 1, 1, 1] -> 3 + 2 + 1 + 1 + 1= 8
[3, 1, 1, 1, 1, 1] -> 3 + 1 + 1 + 1 + 1 + 1= 8
[2, 2, 2, 2] -> 2 + 2 + 2 + 2 = 8
[2, 2, 2, 1, 1] -> 2 + 2 + 2 + 1 + 1 = 8
[2, 2, 1, 1, 1, 1] -> 2 + 2 + 1 + 1 + 1 + 1 = 8
[2, 1, 1, 1, 1, 1, 1] -> 2 + 1 + 1 + 1 + 1 + 1 + 1 = 8
[1, 1, 1, 1, 1, 1, 1, 1] -> 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8
The challenge is to create an efficient function to count the number of partitions for a given integer x. Although there are various approaches to solving this problem, we will explore a recursive one.
Code
First, we will create a function called partitions. This function will take three parameters: ones (a list of ones to be reduced on each iteration), x (the number for which we need to find the partition count), and origin (a list where all the partitions will be stored, which we will modify in-place).
1
2
3
4
5
6
7
8
9
10
11
12
13
def partitions(ones:list, x:int, origin:list=[]) -> list:
total = []
for i in range(ones.count(1),1,-1):
aux = ones[:ones.index(1)]
aux.append(i)
while sum(aux) < x:
aux.append(1)
if not sorted(aux) in origin:
total.append(aux)
origin.append(sorted(aux))
for l in total:
total = total + partitions(l,x,origin)
return total
Next, we create a method named listPartitions that initiates the first call to the partitions function.
1
2
3
4
5
def listPartitions(x:int) -> list:
ones = [1]*x
parts = partitions(ones,x,[])
parts.append(ones)
return parts
To count the partitions, we have the countPartitions function, which simply counts the elements in the partitions list. Please note that this approach consumes a significant amount of memory.
1
2
3
4
5
def countPartitions(x:int) -> int:
if x < 0 or x >= 255:
return -1
else:
return len(listPartitions(x))
Time complexity
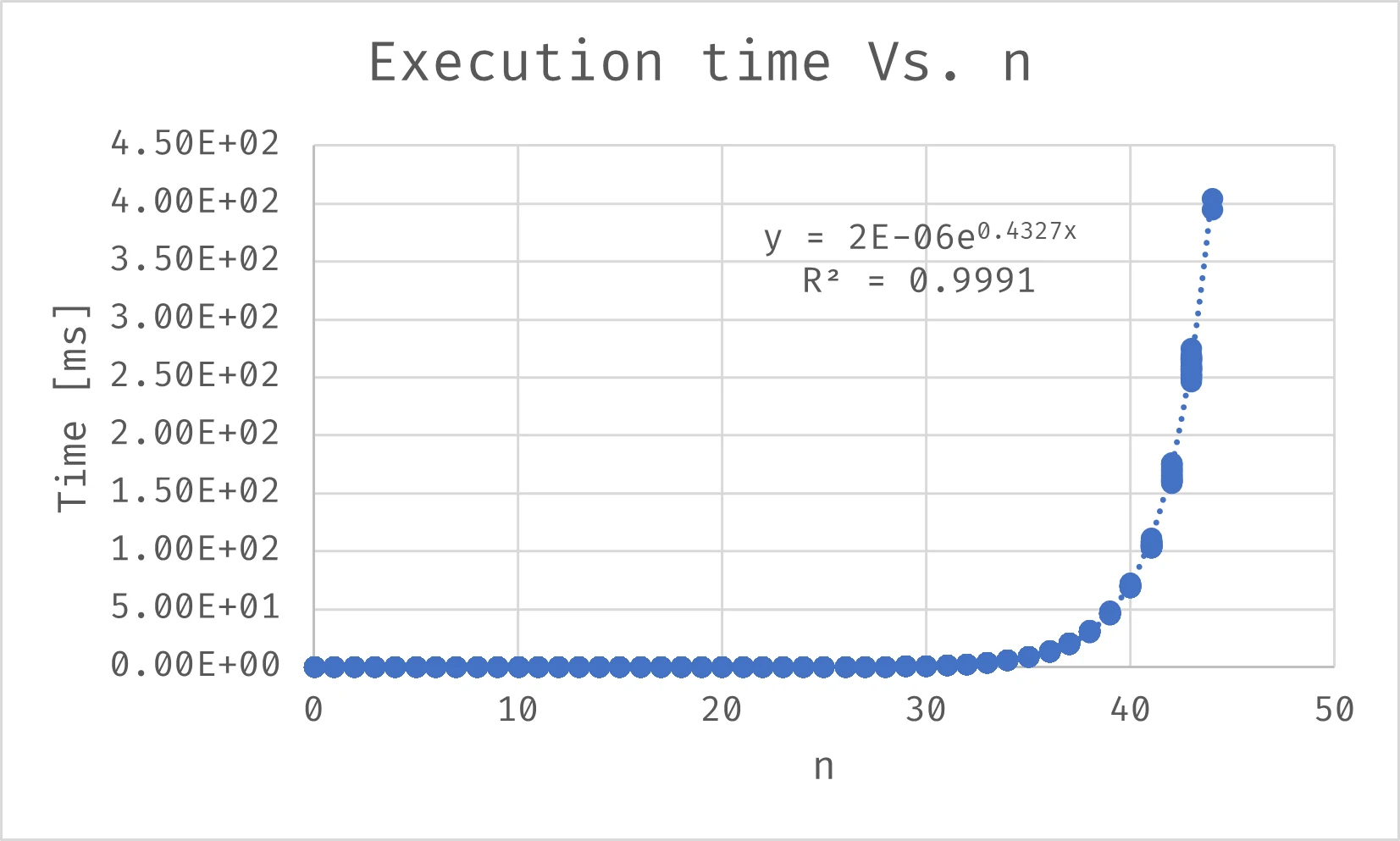
As this approach uses recursion, it’s essential to analyze its time complexity. In a test ranging from n = 0 to n = 44, we can observe that the time required grows exponentially.
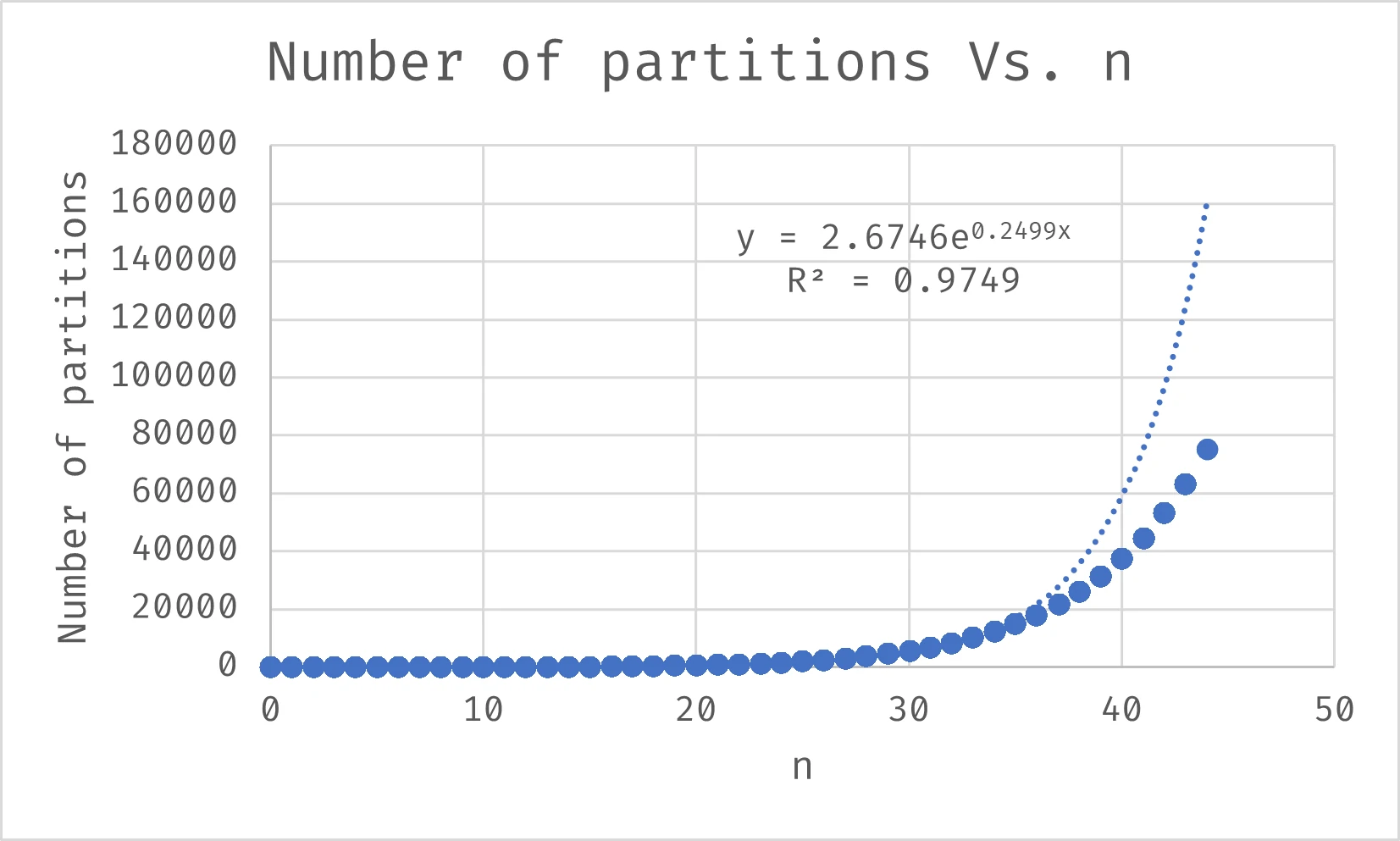
The number of partitions also grows exponentially.
In conclusion, while this recursive algorithm provides a solution, it is not efficient for larger values of x. Feel free to leave your comments and suggestions.